What is RAG?
A Retrieval Augmented Generation (RAG) system is an artificial intelligence framework that enhances the capabilities of large language models (LLMs) by integrating an information retrieval component. Traditionally, LLMs generate responses based solely on the data they were trained on. While this allows them to produce fluent and coherent text, it can sometimes lead to issues like:
- Hallucinations: Generating factually incorrect or nonsensical information.
- Outdated knowledge: Their knowledge is limited to their last training cutoff date.
- Lack of transparency: It's hard to trace the source of their generated information.
How RAG Works
RAG systems address these limitations by first retrieving relevant information from a knowledge base (e.g., a collection of documents, databases, or the internet) and then conditioning the LLM's generation on this retrieved information. This process typically involves two main stages:
Retrieval
When a user poses a query, the RAG system searches its knowledge base for documents or passages that are semantically similar or relevant to the query. This often involves using techniques like vector embeddings and similarity search.
Generation
The retrieved information, along with the original query, is then fed into the LLM as context. The LLM uses this context to generate a more accurate, up-to-date, and grounded response.
The Retrieval Process in Detail
The retrieval phase in RAG systems is a sophisticated process that involves several key steps and algorithms:
1. Document Indexing
Before any retrieval can happen, the knowledge base must be properly indexed. This involves:
- Breaking down documents into manageable chunks
- Creating vector embeddings for each chunk
- Storing these embeddings in a vector database for efficient retrieval
2. Query Processing
When a query is received, it undergoes several processing steps:
- Tokenization and normalization
- Vector embedding creation using the same model as the documents
- Query expansion (optional) to improve recall
3. Similarity Search Algorithms
Several algorithms are commonly used for similarity search:
- Cosine Similarity: Measures the cosine of the angle between vectors
- Euclidean Distance: Measures the straight-line distance between points
- Dot Product: Measures the projection of one vector onto another
- Approximate Nearest Neighbors (ANN): Efficient algorithms for large-scale search
Understanding Vector Representation
Text is converted into vectors through a process called embedding, which captures semantic meaning in a multi-dimensional space.
2D Vector Space
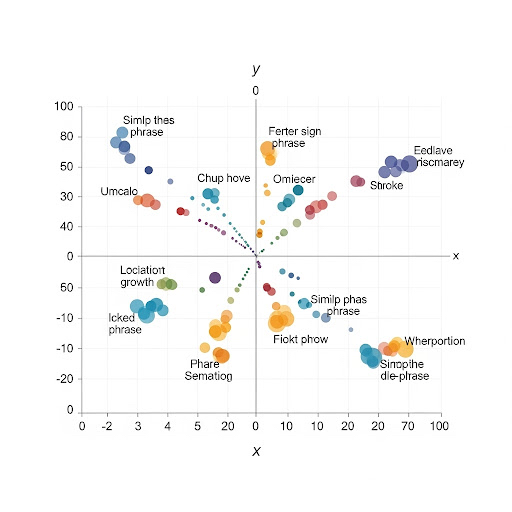
In a simplified 2D space, we can visualize how different words or phrases are positioned relative to each other. Words with similar meanings will be closer together in this space.
Multi-dimensional Space
In reality, embeddings exist in a much higher-dimensional space (often 300-1000 dimensions). This allows for capturing complex relationships and nuances in meaning that can't be represented in 2D or 3D.
How Vector Embeddings Work
Vector embeddings are created through several methods:
- Word2Vec: Creates embeddings by predicting surrounding words
- GloVe: Uses global word co-occurrence statistics
- BERT: Creates contextual embeddings based on surrounding text
- Sentence Transformers: Specialized for creating sentence-level embeddings
Each dimension in the vector represents a different aspect of meaning, and the position of a word or phrase in this space captures its semantic relationships with other words and phrases.
Benefits of RAG Systems
- Improved factual accuracy
- Reduced hallucinations
- Ability to incorporate real-time knowledge
- Enhanced explainability
Implementation Example
Here's a small Python program that takes a query string, evaluates it against other predefined strings within a Cartesian-like scheme, and outputs the most compatible strings with a marginal difference of 0.5.
How It Works
For simplicity, this example uses cosine similarity to assess the compatibility between strings. We represent strings as vectors in a Cartesian space through a TF-IDF vectorization process. This method is commonly used to measure how "similar" two documents (or strings) are based on their word content.
Python Implementation
import numpy as np
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics.pairwise import cosine_similarity
def assess_string_compatibility(query_string, strings_to_evaluate, margin_threshold=0.5):
"""
Assesses the compatibility of a query string with a list of other strings
using cosine similarity on TF-IDF vectors.
Args:
query_string (str): The query string to assess.
strings_to_evaluate (list): A list of strings to compare against the query.
margin_threshold (float): The maximum allowed marginal difference for compatibility.
Returns:
list: A list of tuples (string, similarity) of the most compatible strings.
"""
# Combine all strings to train the TF-IDF vectorizer
all_strings = [query_string] + strings_to_evaluate
# Initialize the TF-IDF vectorizer
# min_df=1 ensures that even words appearing only once are considered
vectorizer = TfidfVectorizer(min_df=1)
# Transform the strings into TF-IDF vectors
tfidf_matrix = vectorizer.fit_transform(all_strings)
# Extract the vector for the query string (the first one in the matrix)
query_vector = tfidf_matrix[0:1]
# Calculate the cosine similarity between the query string and all other strings
similarities = cosine_similarity(query_vector, tfidf_matrix[1:])
# Find the maximum similarity among all evaluated strings
max_similarity = np.max(similarities) if similarities.size > 0 else 0
compatible_strings = []
# Iterate over the similarities and filter those within the margin
for i, sim in enumerate(similarities[0]):
# The compatibility condition is that the similarity is close to the maximum
# with a difference not exceeding the margin_threshold
if (max_similarity - sim) <= margin_threshold:
compatible_strings.append((strings_to_evaluate[i], sim))
# Sort the compatible strings from most to least similar
compatible_strings.sort(key=lambda x: x[1], reverse=True)
return compatible_strings
if __name__ == "__main__":
# Example usage:
existing_strings = [
"The black cat sleeps on the sofa",
"A white dog plays in the park",
"The Siamese cat is resting",
"The man reads a book on the bench",
"A small black kitten is playing with a ball",
"The dog runs fast on the grass",
"An interesting book is on the table"
]
user_request = input("Enter your query: ")
results = assess_string_compatibility(user_request, existing_strings, margin_threshold=0.5)
print("\n--- Compatibility Results ---")
if results:
print(f"Strings most compatible with '{user_request}' (margin 0.5):")
for string, sim in results:
print(f"- '{string}' (Similarity: {sim:.4f})")
else:
print(f"No compatible strings found for '{user_request}' with the specified margin.")Technical Explanation
TF-IDF Vectorization
TfidfVectorizer transforms text strings into a numerical representation (vectors). Each dimension of the vector corresponds to a word in the overall vocabulary of the strings.
The value in each dimension (for each word) reflects the importance of that word in the string (how often it appears in the string relative to how often it appears across all strings). This reduces the weight of common words like "the," "a," "of," which don't carry much meaning.
Cartesian Scheme and Cosine Similarity
Once vectorized, strings can be thought of as points in a multi-dimensional space (a "Cartesian scheme" in a broad sense).
Cosine similarity is a measure of the similarity between two non-zero vectors in an inner product space. It's the cosine of the angle between them. A cosine of 1 means the vectors are identical, 0 means they are orthogonal (uncorrelated), and -1 means they are exactly opposite. In our case, the closer the value is to 1, the more similar the strings are.
Compatibility Assessment
The program calculates the cosine similarity between your query_string and each of the strings_to_evaluate.
It finds the maximum similarity achieved among all evaluated strings.
It then filters out strings that have a similarity falling within the margin_threshold (i.e., their similarity is close to the maximum similarity, with a difference not exceeding 0.5). This means we are looking not just for the most similar string, but all those that are almost equally similar.